Yiming CHEN - 陈亿铭

Appearance

UM-CV 2 Image Classification

About 3644 wordsAbout 12 min

notescomputer-vision

2024-12-20

@Credits: EECS 498.007

Personal work for the assignments of the course: github repo.

This course is basically for beginners, so I will skip basic concepts and complete the notes with copilot.

Image Classification

Problem：The semantic gap between low-level features and high-level concepts, and the computers do not have the intuition to understand the image.

Intro

Challenges

  • intraclass variation
  • fine-grained categories
  • background clutter
  • illumination change: lighting and shadow conditions
  • deformatoion: the object may have various positions
  • occlusion: the object may be partially covered

Scientific Applications

  • medical imaging
  • galaxy classification
  • object detection: classify localized objects
  • image captioning: generate a sentence to describe the image, which can be seen as a classification problem of the next-word prediction
  • Playing Go: classify the next move

An Image Classifier?

def classify(image):
    # Some magic here?
    return label

Approaches: find edges, corners, and other features based on human knowledge... but it is not scalable.

Machine Learning: Data-driven Approach

  1. Collect a dataset of images and labels
  2. Use machine learning to train a classifier
  3. Evaluate the classifier on new images
def train(images, labels):
    # Machine learning
    return model
def predict(model, test_image):
    # Use model to predict labels
    return label

Datasets

The most basic datasets: MNIST, CIFAR-10

  • MNIST: handwritten digits
  • CIFAR-10: 10 classes of objects

Larger datasets:

  • ImageNet: 1000 classes, 1.2 million images
  • COCO: 80 object categories, 300k images
  • MIT Places: 205 scene categories, 2.5 million images
  • LAION-5B: 5.85 billion images

Datasets are getting larger and larger, and the models are getting more and more complex.

Omniglot dataset: 1623 characters from 50 alphabets, 20 examples per character. It is used for few-shot learning. Few-shot learning is a type of machine learning that focuses on learning from a small number of examples. （小样本学习）

First Model: Nearest Neighbor

Metrics: L1 distance, L2 distance, cosine similarity

L1 distance: d1(I1,I2)=∑p∣I1p−I2p∣d_1(I_1, I_2) = \sum_p |I_1^p - I_2^p|

L2 distance: d2(I1,I2)=∑p(I1p−I2p)2d_2(I_1, I_2) = \sqrt{\sum_p (I_1^p - I_2^p)^2}

import numpy as np
class NearestNeighbor:
    def __init__(self):
        pass

    def train(self, X, y):
        self.Xtr = X
        self.ytr = y

    def predict(self, X):
        num_test = X.shape[0]
        Ypred = np.zeros(num_test, dtype=self.ytr.dtype)

        for i in range(num_test):
            distances = np.sum(np.abs(self.Xtr - X[i, :]), axis=1)
            min_index = np.argmin(distances)
            Ypred[i] = self.ytr[min_index]

        return Ypred

Training time: O(1)O(1), Testing time: O(N)O(N)

  1. This is computationally expensive!
  2. Outliers can affect the result significantly.
outlier examples
Fig: outliers

Web demo: Nearest Neighbor Demo

Hyperparameters

What is the best K to use?

Hyperparameters: parameters that are not learned by the model, but are set at the start of the learning process.

Setting Hyperparameters:

  • Idea 1: Choose hyperparamters that work best on the data.
    • BAD: This works best on the training data.
  • Idea 2: Split data into train and test and choose hyperparameters that work best on the test data.
    • BAD: The algorithm is polluted by the test data!
  • Idea 3: Split data into train, validation, and test. Choose hyperparameters that work best on the validation data.
    • Better and correst ! We only touch once the test data.
    • Bad perfomance on the test set implies bad performance on the real world.
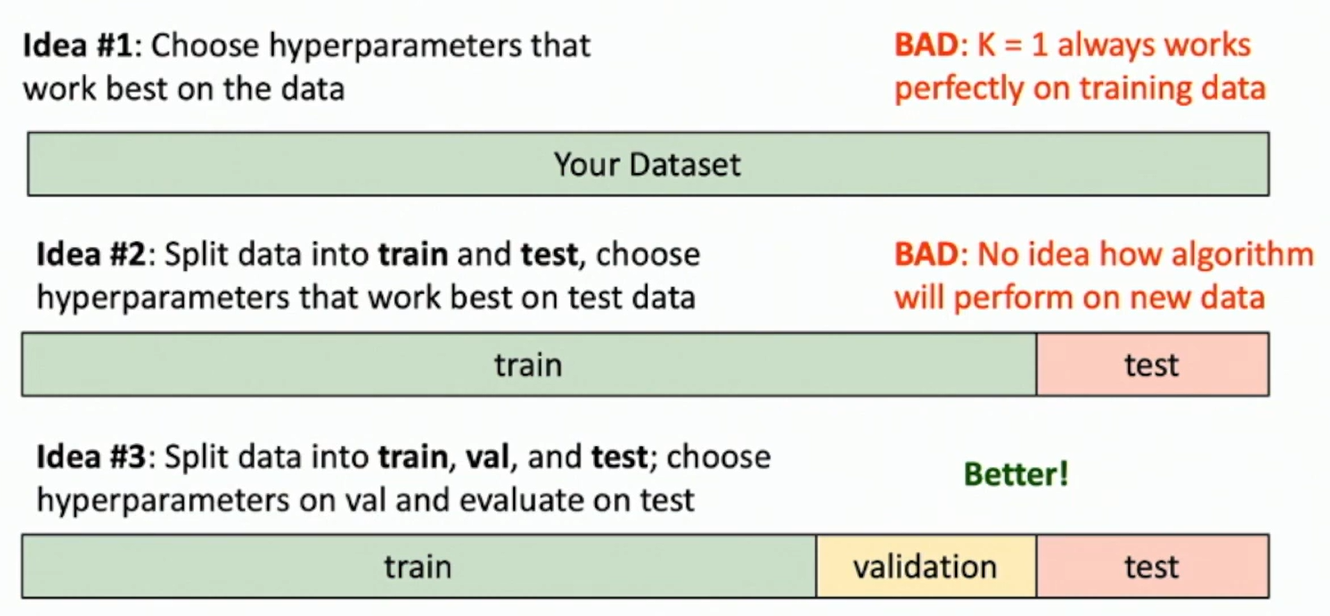
How to split your data
Fig: How to split your data
  • Idea 4: Cross-validation: split data into k folds, train on k-1 folds, and test on the remaining fold. Repeat k times and average the results.
    • Better than Idea 3, but computationally expensive. Useful for small datasets, but not used too much in deep learning.
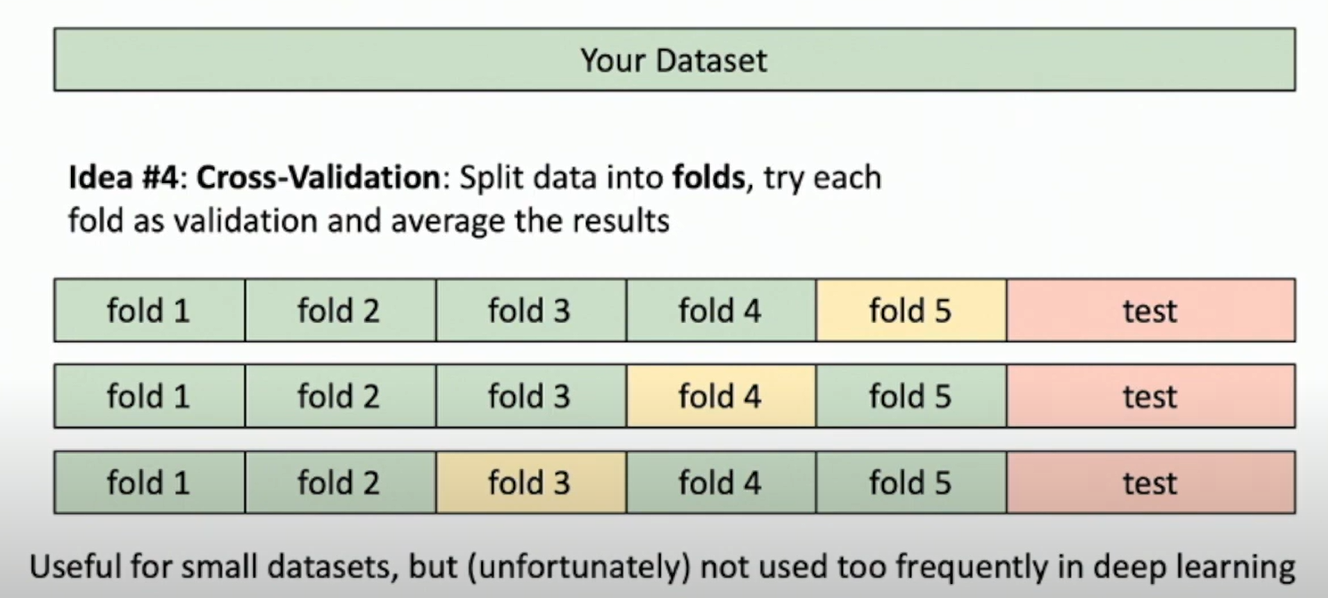
cross-validation
Fig: cross-validation

Emprirical studies:

Emprirical studies
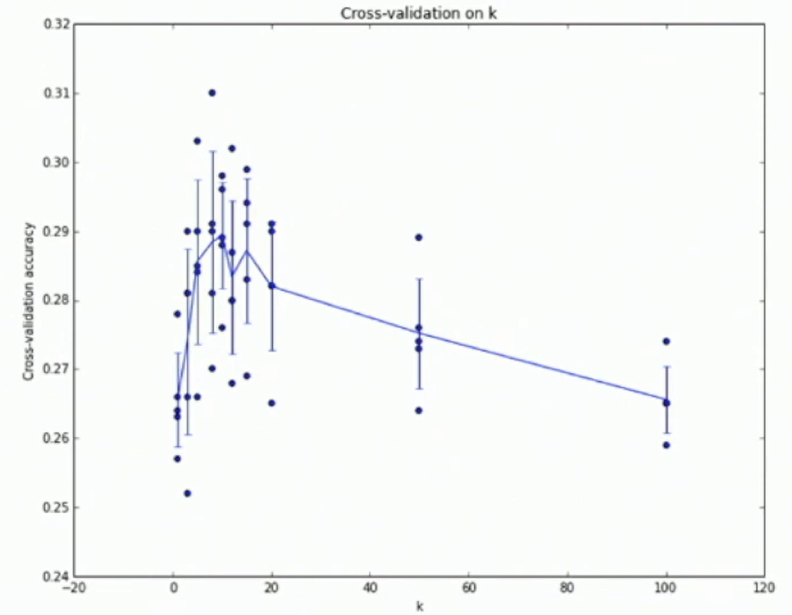
Fig: Emprirical studies

Correctness: Universal Approximation

KNN has universal approximaton power on compact sets.

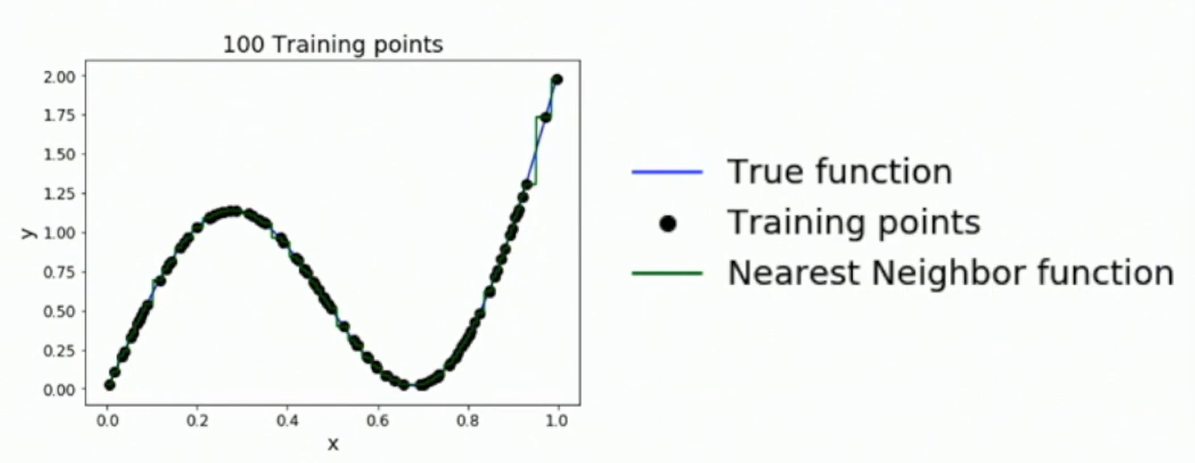
Universal Approximation
Fig: Universal Approximation

Curse of Dimensionality

As the number of (input) dimensions increases, the volume of the space increases exponentially, and the number of data points required to fill the space increases exponentially.

Summary

  • KNN very is slow at runtime.
  • Distance metrics on pixels are not informative, e.g. predicting a human's face based on the surrounding pixels.
  • Surprisingly, KNN works well with extracted convolutional features!

Assignment 1

Some notes:

Access a single row or colums of a tensor

There are two common ways to access a single row or column of a tensor: using an integer will reduce the rank by one, and using a length-one slice will keep the same rank. Note that this is different behavior from MATLAB.

Slicing a tensor

Slicing a tensor returns a view into the same data, so modifying it will also modify the original tensor. To avoid this, you can use the clone() method to make a copy of a tensor.

When you index into torch tensor using slicing, the resulting tensor view will always be a subarray of the original tensor. This is powerful, but can be restrictive.

Indexing with an integer array or a tensor

We can also use index arrays to index tensors; this lets us construct new tensors with a lot more flexibility than using slices.

As an example, we can use index arrays to reorder the rows or columns of a tensor:

# Credit: UMich EECS 498.007

# Create the following rank 2 tensor with shape (3, 4)
# [[ 1  2  3  4]
#  [ 5  6  7  8]
#  [ 9 10 11 12]]
a = torch.tensor([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
print('Original tensor:')
print(a)

# Create a new tensor of shape (5, 4) by reordering rows from a:
# - First two rows same as the first row of a
# - Third row is the same as the last row of a
# - Fourth and fifth rows are the same as the second row from a
idx = [0, 0, 2, 1, 1]  # index arrays can be Python lists of integers
print('\nReordered rows:')
print(a[idx])

# Create a new tensor of shape (3, 4) by reversing the columns from a
idx = torch.tensor([3, 2, 1, 0])  # Index arrays can be int64 torch tensors
print('\nReordered columns:')
print(a[:, idx])

More generally, given index arrays idx0 and idx1 with N elements each, a[idx0, idx1] is equivalent to:

# Credit: UMich EECS 498.007

torch.tensor([
  a[idx0[0], idx1[0]],
  a[idx0[1], idx1[1]],
  ...,
  a[idx0[N - 1], idx1[N - 1]]
])

(A similar pattern extends to tensors with more than two dimensions)

# Credit: UMich EECS 498.007

We can for example use this to get or set the diagonal of a tensor:

a = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print('Original tensor:')
print(a)

idx = [0, 1, 2]
print('\nGet the diagonal:')
print(a[idx, idx])

# Modify the diagonal
a[idx, idx] = torch.tensor([11, 22, 33])
print('\nAfter setting the diagonal:')
print(a)

Select one element from each row or column of a tensor:

Boolean masking of tensors

The shape of the boolean mask should be the same as the original tensor, or should be broadcastable to the same shape. This is commnly used so I will not detail it here.

Contiguous ?

Some combinations of reshaping operations will fail with cryptic errors. The exact reasons for this have to do with the way that tensors and views of tensors are implemented, and are beyond the scope of this assignment. However if you're curious, this blog post by Edward Yang gives a clear explanation of the problem.

pytorch-internals is a good blog to understand the operation contiguous(), view() and reshape().

KNN

Recall: some useful functions in PyTorch

torch.view
torch.reshape
torch.flatten

torch.permute
torch.transpose

torch.squeeze
torch.unsqueeze

torch.argmax
torch.topk
torch.sort
torch.argsort

torch.mm
torch.mv
torch.einsum

torch.cat
torch.chunk

KNN Implementation