UM-CV 5 Neural Networks
@Credits: EECS 498.007
Video Lecture: UM-CV 5 Neural Networks
Neural Networks
Linear classifiers are limited to their linear decision boundaries. Neural networks are more flexible and can learn more complex decision boundaries.
Feature extraction
Color histograms, HOG, SIFT, etc. (2000-2010)
- Color histograms - Statiscal Method
- HOG: Histogram of Oriented Gradients
- Compute edge direction/strength at each pixel
- Bag of Words(Data-Driven) - Clustering
- Extract random patches from images &Cluster patches into "codebook" of visual words
- Encode each image as histogram of visual words
- Concatenate features together - Different methods can capture different features of the image
2011 ImageNet Winner: A complicated feature extractor
SIFT: Scale-Invariant Feature Transform 128-D vector
color: 96-D vector
Reduced to 64-D with PCA
FV extraction and compression
One-vs-all SVM learning with SGD
Late fusion of SIFT and color systems
Problem: These complicated systems are not designed to directly minimize the classification error!
AlexNet: Deep Learning (2012)
Deep Neural Networks (DNNs) are end-to-end trainable!
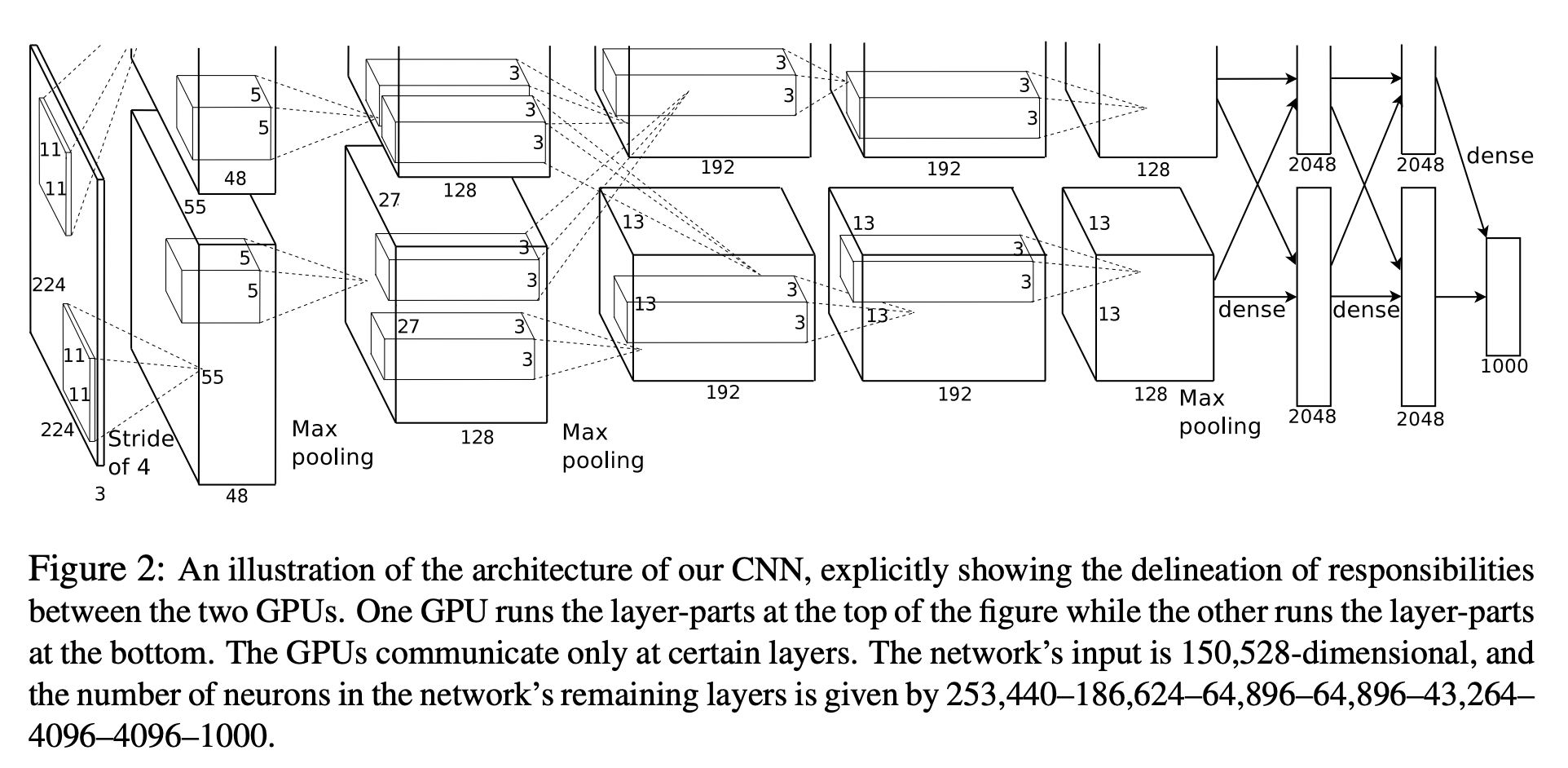
Fig: AlexNet
Neural Networks
(Before) Linear score function: f(x,W)=Wx
(Now) 2-layer Neural Network: f(x,W)=W2max(0,W1x)
where x∈RD,W1∈RH×D, W2∈RC×H
or 3-layer Neural Network
f(x,W)=W3max(0,W2max(0,W1x))
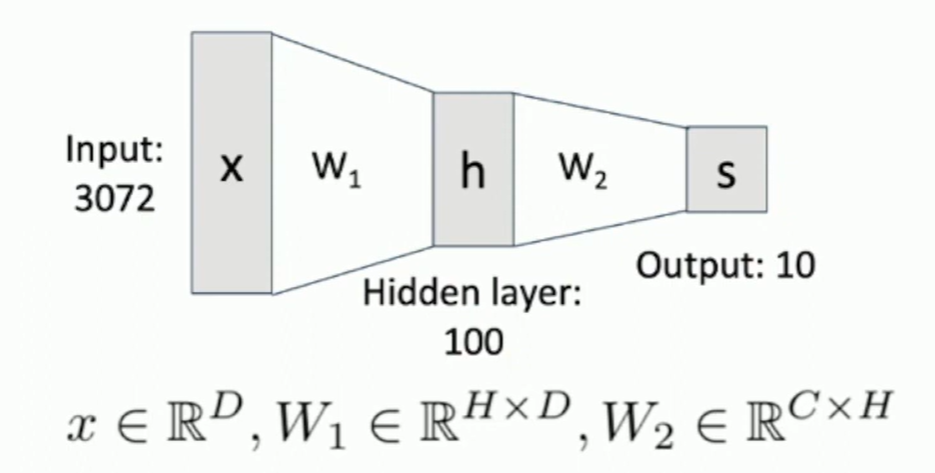
Fig: Data Flow
Deep Neural Networks
Each output is affected by each input: Fully connected network (or MLP - Multi-Layer Perceptron), and templates (each row of the matrix W) are combined layerwise.
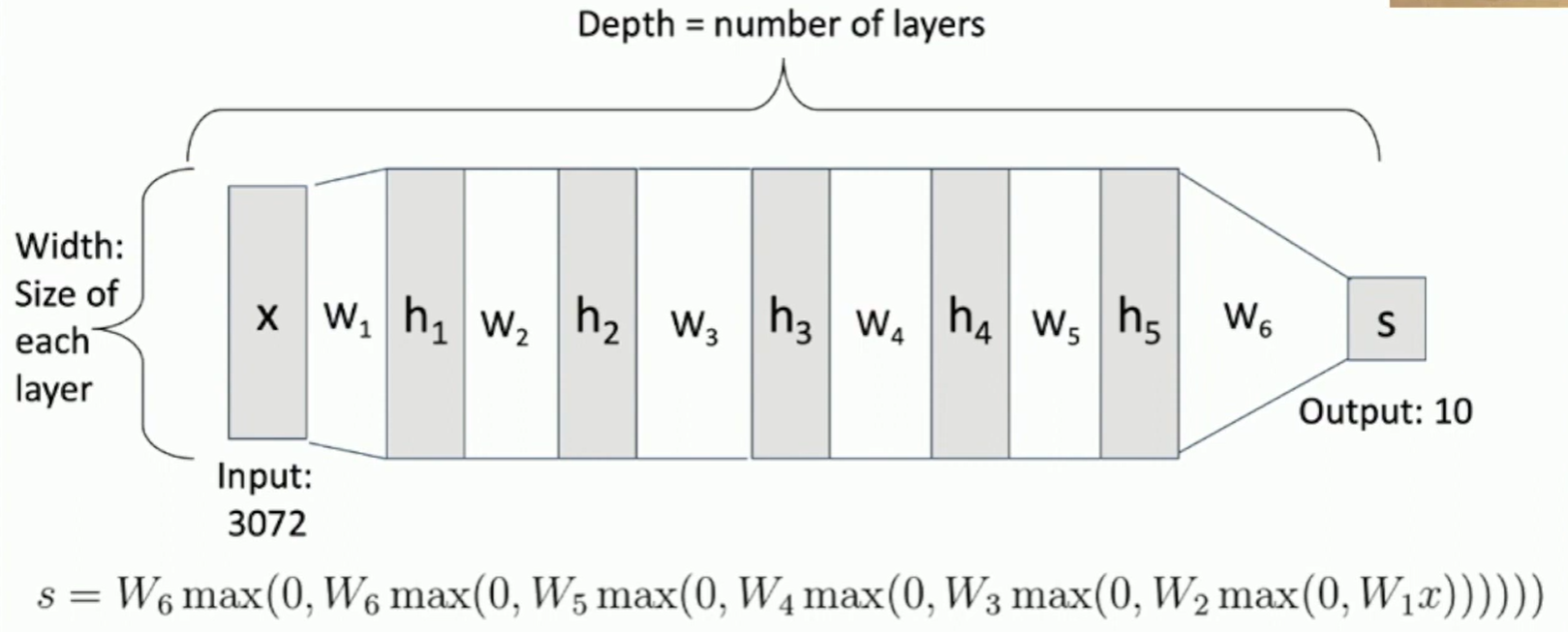
Fig: DNN
Activation Functions
Add non-linearity to the network. Without non-linearity, the network would be equivalent to a single layer.
The most widely used: ReLU (Rectified Linear Unit)
ReLu(x)=max(0,x)
Sigmoid
σ(x)=1+e−x1
Tanh
tanh(x)=ex+e−xex−e−x
Leaky ReLU
Leaky ReLU(x)=max(0.01x,x)
Maxout
Maxout(x)=max(w1Tx+b1,w2Tx+b2)
ELU
ELU(x)={xα(ex−1)if x>0if x≤0
Neural Network in < 20 lines!
import numpy as np
from numpy.random import randn
N, Din, H, Dout, = 64, 1000, 100, 10
x, y = randn(N, Din), randn(N, Dout)
w1, w2 = randn(Din, H), randn(H, Dout)
learning_rate = 1e-6
for t in range(10000):
h = 1/(1 + np.exp(-x.dot(w1)))
y_pred = h.dot(w2)
loss = np.square(y_pred - y).sum()
grad_y_pred = 2.0 * (y_pred - y)
grad_w2 = h.T.dot(grad_y_pred)
grad_h = grad_y_pred.dot(w2.T)
grad_w1 = x.T.dot(grad_h * h * (1 - h))
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2Analogy: Biological Neurons
Our brains are made of neurons. Impulses are carried away from cell body. Dendrites receive impulses from other neurons. Synapses are connections between neurons.
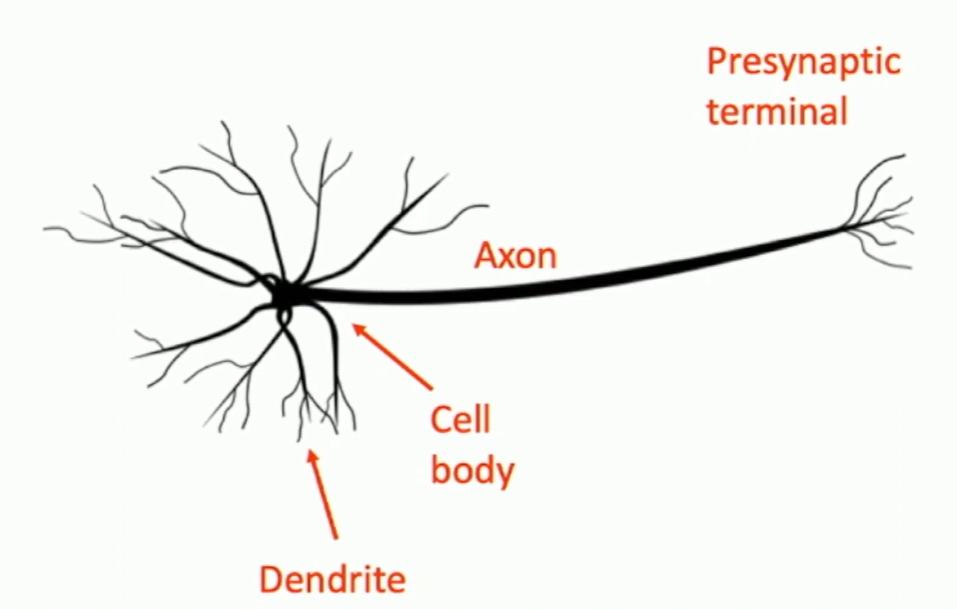
Fig: Biological Neurons
Differences between biological and artificial neurons
- Biological neurons have complex connectivity patterns
- Inside a neuron, signals are computated by complex processes
- Artificial neurons are organized into regular layers for computational efficiency
Fun fact: But neural networks with random connectivity can still learn!
Space Warping
A linear layer cannot improve the representation power of the classifier, but with a non-linear transform in between, the classifier can learn more complex decision boundaries.
Explanation: Space Warping
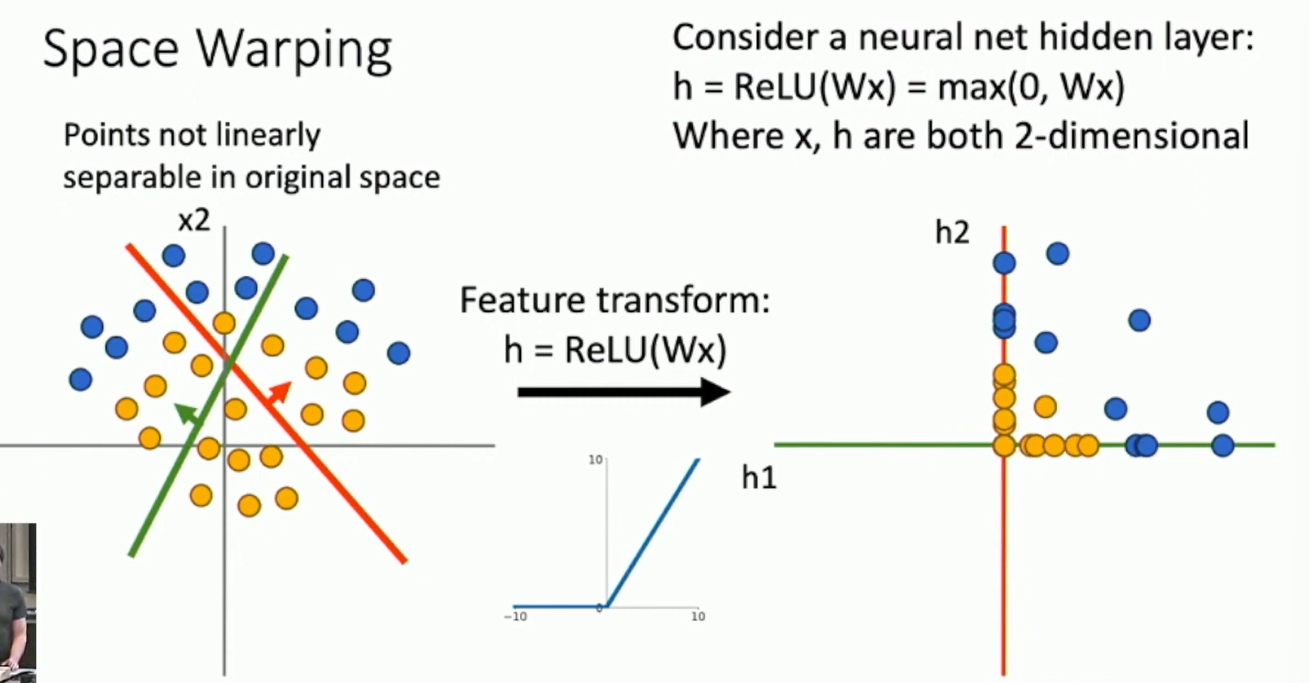
Fig: Space Warping
Points can be linearly separable in a higher-dimensional space.
Technique: Don't regularize with size; instead use stronger L2.
Universal Approximation
A neural network with a single hidden layer can approximate any continuous function to arbitrary accuracy (uniformly convergent), on compacts of Rn.
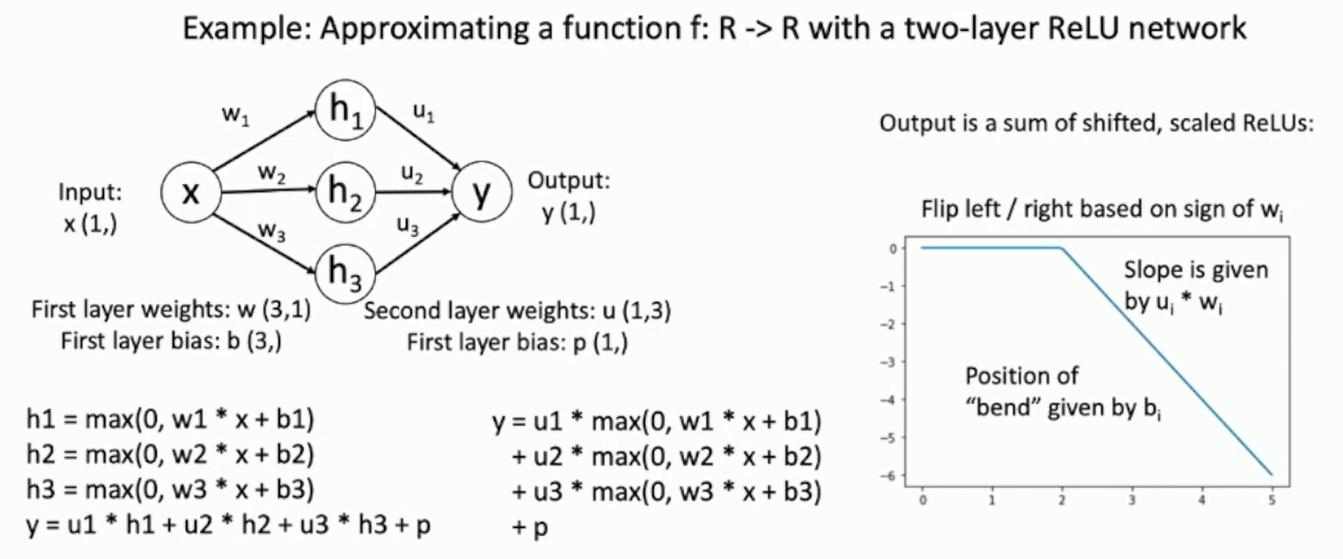
Fig: Universal Approximation
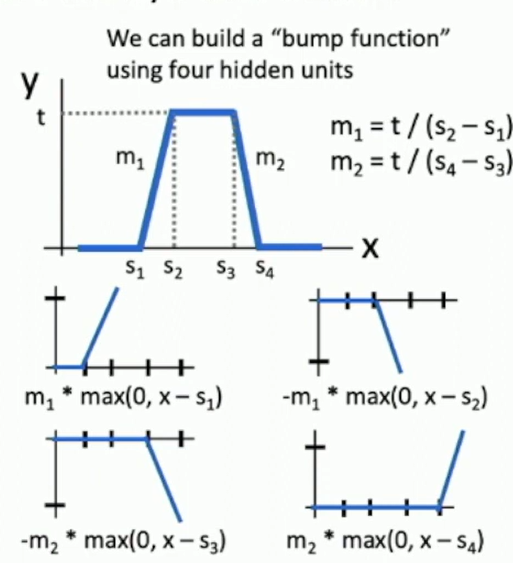
Fig: Bump function as basis
See Nielsen's Neural Networks and Deep Learning for more details.
Reality check: Networks don't really learn bumps!
But the theorem does not tell us how to find the right weights, given that f is unknown a priori.
Convergence of Neural Networks
Definition: (Convexity) A function f:RD→R is convex if for all x,y∈RD and t∈[0,1], we have
f(tx+(1−t)y)≤tf(x)+(1−t)f(y)
Theorem: Linear networks are convex in the weights.
No such guarantee for non-linear networks.
Neural net losses sometimes look convex-ish.
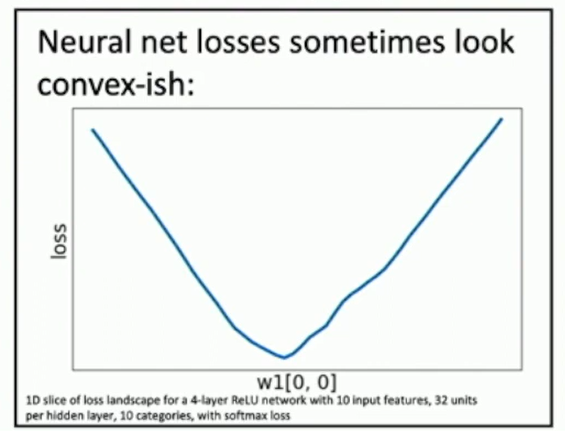
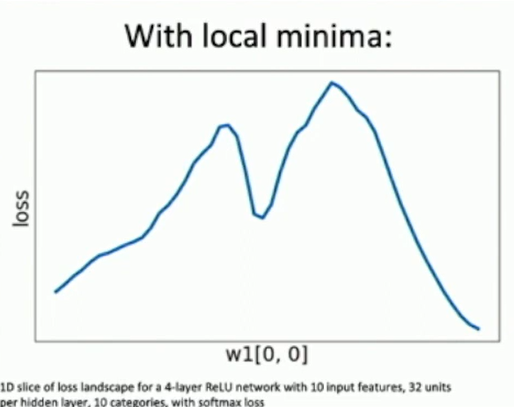
Fig: loss surfaces
Open question: theorectical properties of the optimization landscape of neural networks.
Summary
- Feature transform
- Neural networks
- Activation functions
- Biological neurons
- Space warping
- Universal approximation
- Convergence of neural networks