For the rules of matrix differentiation, please refer to the previous article: Calculate the gradient of a matrix by hand in deep learning

Recall of essential rules

Let $X$ be a matrix of size $m \times n$, and $L$ be a scalar function of $X$.

In higher order notation, we introduce the concept of differentials. If $L$ is differentiable, then for a small change $dX$ in the matrix $X$, we have

$$dL = \sum_{i=1}^m \sum_{j=1}^n \frac{\partial L}{\partial X_{i,j}} \, dX_{i,j}$$

where $dX_{i,j}$ is a small change (well actually this is a linear functional) in the element $X_{i,j}$.

And we define the matrix of partial derivatives as

$$\frac{\partial L}{\partial X} = \begin{bmatrix} \frac{\partial L}{\partial X_{1,1}} & \cdots & \frac{\partial L}{\partial X_{1,n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial L}{\partial X_{m,1}} & \cdots & \frac{\partial L}{\partial X_{m,n}} \end{bmatrix}$$

Then we can write the differential as a Frobenius product:

Important Frobenius product

We will use this following formula many times in the next sections.

We can write $dL$ as a Frobenius product of the gradient of $L$ and the differential of $X$.

$$dL = \mathrm{tr}\left(\left(\frac{\partial L}{\partial X}\right)^\top \, dX\right)$$

This is obtained by the fact that $\mathrm{tr}(A^\top B)=A_{i,j}B_{i,j}$.

where $dX$ is a matrix of the same shape as $X$, representing the differential (or a small variation) of $X$.

Differential rules

Tricks

$$\begin{align*} &d(X\pm Y) = dX \pm dY \\ &d(XY) = X \, dY + Y \, dX \\ &d(X^\top) = (dX)^\top \\ &d(\mathrm{tr}(X)) = \mathrm{tr}(dX) \\ \end{align*}$$

If $X$ is invertible, then we have

$$\begin{align*} &d(X^{-1}) = -X^{-1} \, dX \, X^{-1} \\ &d(\det(X)) = \det(X) \, \mathrm{tr}(X^{-1} \, dX)\\ \end{align*}$$

Element-wise operations:

$$\begin{align*} &d(X \odot Y) = Y \odot dX + X \odot dY \\ &d(X \oslash Y) = \frac{dX \odot Y - X \odot dY}{Y^2} \\ \end{align*}$$

Element-wise functions:

$$d\sigma(X) = \sigma'(X) \odot dX$$

Trace rules

Tricks

1. Scalar rule: if $a$ is a scalar, then $\mathrm{tr}(a) = a$.
2. Transpose rule: $\mathrm{tr}(A) = \mathrm{tr}(A^\top)$.
3. Linearity: $\mathrm{tr}(A + B) = \mathrm{tr}(A) + \mathrm{tr}(B)$.
4. Cyclic rule: $\mathrm{tr}(AB) = \mathrm{tr}(BA)$.
5. Product rule: $\mathrm{tr}(A^\top (B \odot C)) = \mathrm{tr}((A \odot B)^\top C)$.

Batch normalization differentiation by hand

The gradient of batch normalization is notoriously difficult to calculate. Our method simplify the calculation of the gradient of batch normalization, and we will just apply the rules.

We will define the following variables:

• $X$: input data, $X \in \mathbb{R}^{N \times D}$
• $\mu$ : mean of $X$, $\mu \in \mathbb{R}^{D}$, a row vector
• $\sigma^2$ : variance of $X$, $\sigma^2 \in \mathbb{R}^{D}$, a row vector
• $\hat{X}$ : normalized data, $\hat{X} \in \mathbb{R}^{N \times D}$
• $\mathbf{1}_N$: a column vector of ones, $\mathbf{1}_N \in \mathbb{R}^{N}$
• $L$: loss function, $L \in \mathbb{R}$

As well as the following parameters:

• $\gamma$ : scale parameter, $\gamma \in \mathbb{R}^{D}$, a row vector
• $\beta$ : shift parameter, $\beta \in \mathbb{R}^{D}$, a row vector

Forward pass

The forward pass of batch normalization is as follows:

$$\begin{aligned} \mu &= \frac{1}{N} X_i \\ \sigma^2 &= \frac{1}{N} \sum_{i=1}^{N} (X_i - \mu)^2 \\ \hat{X} &= \frac{X - \mu}{\sqrt{\sigma^2 + \epsilon}} \end{aligned}$$

Vectorized form:

$$\begin{aligned} \mu &= \frac{1}{N} \mathbf{1}_N^\top X \\ \sigma^2 &= \frac{1}{N} \mathbf{1}_N^\top (X - \mathbf{1}_N\mu)^2 \\ \hat{X} &= \frac{X - \mathbf{1}_N\mu}{\sqrt{\mathbf{1}_N\sigma^2 + \epsilon}} \\ Y &= (\mathbf{1}_N \gamma) \odot\hat{X} + \mathbf{1}_N\beta \end{aligned}$$

The computational graph is shown below:

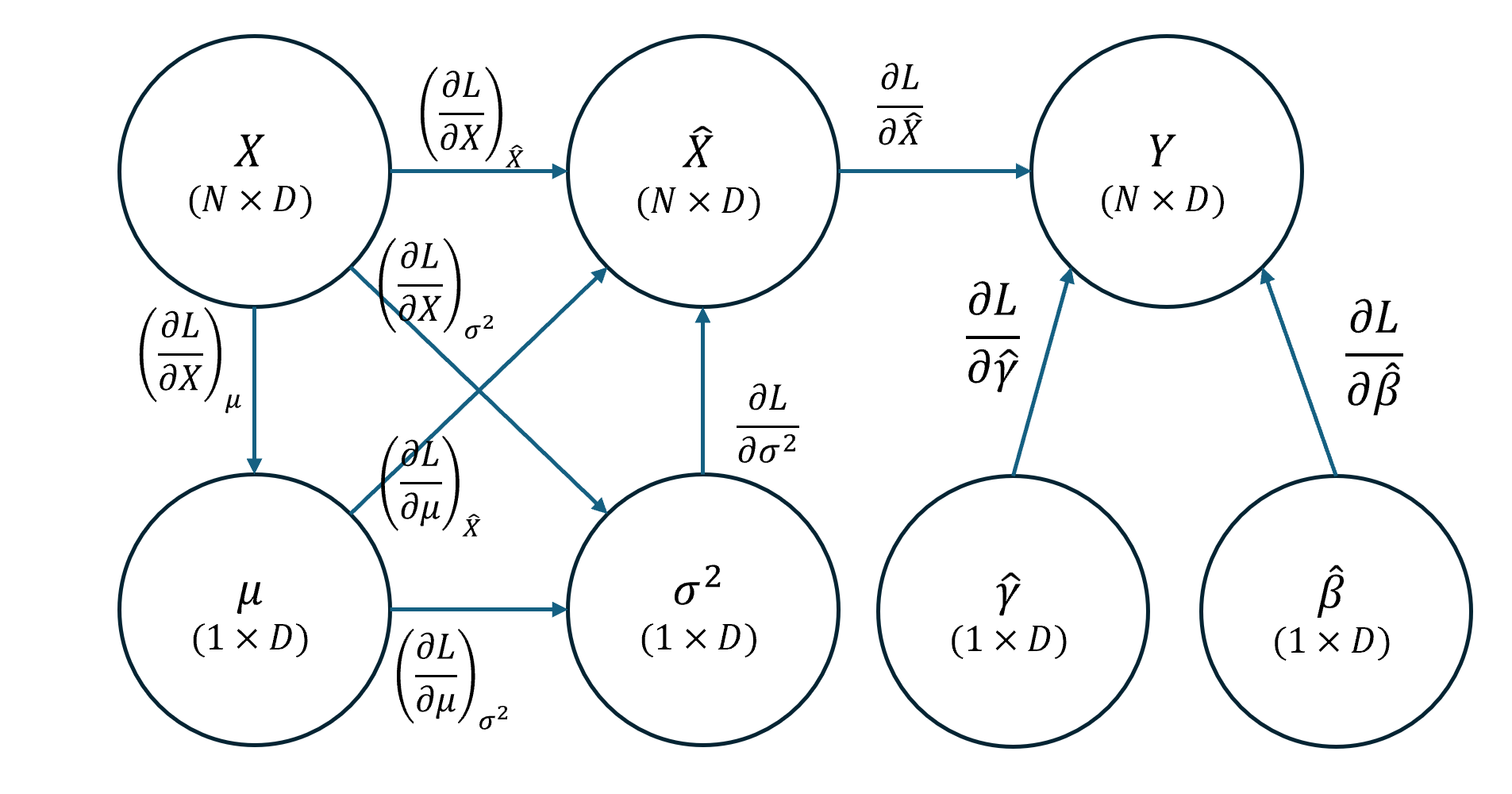
Fig: Computational graph

Backward pass

Suppose we have the upstream gradient $\frac{\partial L}{\partial Y}$

Step 1: Backpropagate Y

Calculate $\frac{\partial L}{\partial \beta}$, $\frac{\partial L}{\partial \gamma}$, $\frac{\partial L}{\partial \hat{X}}$

Recall the formula of $Y$:

$$Y = (\mathbf{1}_N \gamma) \odot\hat{X} + \mathbf{1}_N\beta$$

We have the differential of $Y$:

$$dY = (\mathbf{1}_N d\gamma) \odot\hat{X} + (\mathbf{1}_N \gamma) \odot d\hat{X} + \mathbf{1}_N d\beta$$

We can write the differential of $L$ as a Frobenius product:

$$\begin{aligned} dL &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial Y}\right)^\top dY\right) \\ &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial Y}\right)^\top\left((\mathbf{1}_N d\gamma) \odot\hat{X} + (\mathbf{1}_N \gamma) \odot d\hat{X} + \mathbf{1}_N d\beta\right)\right) \\ &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial Y}\right)^\top (\mathbf{1}_N d\gamma) \odot\hat{X}\right) + \mathrm{tr}\left(\left(\frac{\partial L}{\partial Y}\right)^\top (\mathbf{1}_N \gamma) \odot d\hat{X}\right) + \mathrm{tr}\left(\left(\frac{\partial L}{\partial Y}\right)^\top \mathbf{1}_N d\beta\right) \\ &= \mathrm{tr}\left(\left(\mathbf{1}_N^\top\frac{\partial L}{\partial Y}\right)^\top d\gamma \odot\hat{X}\right) + \mathrm{tr}\left(\left(\frac{\partial L}{\partial Y}\right)^\top (\mathbf{1}_N \gamma) \odot d\hat{X}\right) + \mathrm{tr}\left(\left(\frac{\partial L}{\partial Y}\right)^\top \mathbf{1}_N d\beta\right) \\ \end{aligned}$$

For the first term, we have:

$$\begin{aligned} dL' &= \mathrm{tr}\left(\left(\mathbf{1}_N^\top\frac{\partial L}{\partial Y}\right)^\top d\gamma \odot\hat{X}\right) \\ &= \mathrm{tr}\left(\left(\mathbf{1}_N^\top\frac{\partial L}{\partial Y}\right)^\top \hat{X} \odot d\gamma \right) \\ &= \mathrm{tr}\left(\left(\hat{X}^\top\mathbf{1}_N^\top\frac{\partial L}{\partial Y}\right)^\top d\gamma \right) \\ \end{aligned}$$

Thus, $\frac{\partial L}{\partial \gamma} = \hat{X}^\top\mathbf{1}_N^\top\frac{\partial L}{\partial Y}$

For the second term, we have:

$$\begin{aligned} dL'' &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial Y}\right)^\top (\mathbf{1}_N \gamma) \odot d\hat{X}\right) \\ \end{aligned}$$

by applying the product rule, we have:

$$\begin{aligned} dL'' &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial Y}\right)^\top (\mathbf{1}_N \gamma) \odot d\hat{X}\right) \\ &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial Y} \odot \mathbf{1}_N \gamma\right)^\top d\hat{X}\right) \\ \end{aligned}$$

Thus $\frac{\partial L}{\partial \hat{X}} = \frac{\partial L}{\partial Y} \odot \mathbf{1}_N \gamma$

For the third term, similarly, we have:

$$\begin{aligned} \frac{\partial L}{\partial \beta} &= \mathbf{1}_N^\top\frac{\partial L}{\partial Y} \end{aligned}$$

Step 2: Backpropagate X_hat

Now that we have $\frac{\partial L}{\partial \hat{X}}$, we can calculate $\frac{\partial L}{\partial \mu}$ and $\frac{\partial L}{\partial \sigma^2}$.

Recall the rules:

$$\begin{align*} &d(X \odot Y) = Y \odot dX + X \odot dY \\ &d(X \oslash Y) = \frac{dX \odot Y - X \odot dY}{Y^2} \\ &d\sigma(X) = \sigma'(X) \odot dX \end{align*}$$

and the definition of $\hat{X}$:

$$\hat{X} = \frac{X - \mathbf{1}_N\mu}{\sqrt{\mathbf{1}_N\sigma^2 + \epsilon}}$$

we have

$$\begin{aligned} d\hat{X} &= d(\frac{X - \mathbf{1}_N\mu}{\sqrt{\mathbf{1}_N\sigma^2 + \epsilon}}) \\ &= \frac{d(X-\mathbf{1}_N\mu)\odot\sqrt{1_N\sigma^2+\epsilon}-(X-\mathbf{1}_N\mu)\odot d(\sqrt{\mathbf{1_N}\sigma^2+\epsilon})}{\mathbf{1}_N\sigma^2+\epsilon} \\ &= \frac{dX-\mathbf{1}_Nd\mu}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}} - \frac{(X-\mathbf{1}_N\mu)\odot\frac{1}{2}(\mathbf{1}_N\sigma^2+\epsilon)^{-\frac{1}{2}}\odot d(\mathbf{1}_N\sigma^2+\epsilon)}{\mathbf{1}_N\sigma^2+\epsilon} \\ &= \frac{dX-\mathbf{1}_Nd\mu}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}} - \frac{(X-\mathbf{1}_N\mu)}{2(\mathbf{1}_N\sigma^2+\epsilon)^{\frac{3}{2}}}\odot (\mathbf{1}_N d\sigma^2) \end{aligned}$$

Abuse of notation: we will use $dL$ to denote a part of the real $dL$, since wo do not care about the differential with respect to $\gamma$ and $\beta$

Meanwhile, we have

$$\begin{aligned} dL &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial \hat{X}}\right)^\top d\hat{X}\right) \\ \end{aligned}$$

by developing $d\hat{X}$, we have

$$\begin{aligned} dL &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial \hat{X}}\right)^\top \left(\frac{dX-\mathbf{1}_Nd\mu}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}} - \frac{(X-\mathbf{1}_N\mu)}{2(\mathbf{1}_N\sigma^2+\epsilon)^{\frac{3}{2}}}\odot (\mathbf{1}_N d\sigma^2)\right)\right) \\ &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial \hat{X}}\right)^\top \frac{dX-\mathbf{1}_Nd\mu}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}}\right) - \mathrm{tr}\left(\left(\frac{\partial L}{\partial \hat{X}}\right)^\top \frac{(X-\mathbf{1}_N\mu)}{2(\mathbf{1}_N\sigma^2+\epsilon)^{\frac{3}{2}}}\odot (\mathbf{1}_N d\sigma^2)\right) \\ \end{aligned}$$

where we can clearly see $dX$, $d\mu$ and $d\sigma^2$. But be careful $d\mu$ contains $dX$. And since the differential is linear, we add all gradients together later on.

Continue developing the formula above, we have

$$\begin{aligned} dL &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial \hat{X}}\right)^\top \frac{dX}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}}\right) - \mathrm{tr}\left(\left(\frac{\partial L}{\partial \hat{X}}\right)^\top \frac{\mathbf{1}_Nd\mu}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}}\right) \\ \quad &- \mathrm{tr}\left(\left(\frac{\partial L}{\partial \hat{X}}\right)^\top \frac{(X-\mathbf{1}_N\mu)}{2(\mathbf{1}_N\sigma^2+\epsilon)^{\frac{3}{2}}}\odot (\mathbf{1}_N d\sigma^2)\right) \\ \end{aligned}$$

The first term gives a part of the gradient of $X$:

$$\begin{aligned} \left(\frac{\partial L}{\partial X}\right)_{\hat{X}} &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial \hat{X}} \odot \frac{1}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}}\right)^\top dX \right) \\ \end{aligned}$$

Thus, $\frac{\partial L}{\partial X} = \frac{\partial L}{\partial \hat{X}} \odot \frac{1}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}}$

The second term gives a part of the gradient of $\mu$:

$$\begin{aligned} \left(\frac{\partial L}{\partial \mu}\right)_{\hat{X}} &= \mathrm{tr}\left(\left(-\mathbf{1}_N^\top\left(\frac{\partial L}{\partial \hat{X}} \odot \frac{1}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}}\right)\right)^\top d\mu \right) \\ \end{aligned}$$

Thus, $\frac{\partial L}{\partial \mu} = -\mathbf{1}_N^\top\left(\frac{\partial L}{\partial \hat{X}} \odot \frac{1}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}}\right)$

The third term gives the gradient of $\sigma^2$:

$$\begin{aligned} \frac{\partial L}{\partial \sigma^2} &= \mathrm{tr}\left(\left(-\mathbf{1}_N^\top\left(\frac{\partial L}{\partial \hat{X}} \odot \frac{(X-\mathbf{1}_N\mu)}{2(\mathbf{1}_N\sigma^2+\epsilon)^{\frac{3}{2}}}\right)\right)^\top d\sigma^2 \right) \\ \end{aligned}$$

Thus $\frac{\partial L}{\partial \sigma^2} = -\mathbf{1}_N^\top\left(\frac{\partial L}{\partial \hat{X}} \odot \frac{(X-\mathbf{1}_N\mu)}{2(\mathbf{1}_N\sigma^2+\epsilon)^{\frac{3}{2}}}\right)$

Step 3: Backpropagate σ2

Recall the formula of $\sigma^2$:

$$\begin{aligned} \sigma^2 &= \frac{1}{N} \mathbf{1}_N^\top (X - \mathbf{1}_N\mu)^2 \\ \end{aligned}$$

Hence,

$$\begin{aligned} d\sigma^2 &= \frac{1}{N} \mathbf{1}_N^\top d(X - \mathbf{1}_N\mu)^2 \\ &= \frac{1}{N} \mathbf{1}_N^\top 2(X - \mathbf{1}_N\mu) \odot d(X - \mathbf{1}_N\mu) \\ &= \frac{2}{N} \mathbf{1}_N^\top (X - \mathbf{1}_N\mu) \odot d(X - \mathbf{1}_N\mu) \\ \end{aligned}$$

Therefore,

$$\begin{aligned} dL &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial \sigma^2}\right)^\top d\sigma^2\right) \\ &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial \sigma^2}\right)^\top \frac{2}{N} \mathbf{1}_N^\top (X - \mathbf{1}_N\mu) \odot d(X - \mathbf{1}_N\mu)\right) \\ &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial \sigma^2}\right)^\top \frac{2}{N} \mathbf{1}_N^\top (X - \mathbf{1}_N\mu) \odot dX\right) \\ & \quad - \mathrm{tr}\left(\left(\frac{\partial L}{\partial \sigma^2}\right)^\top \frac{2}{N} \mathbf{1}_N^\top (X - \mathbf{1}_N\mu) \odot d\mu\right) \\ \end{aligned}$$

For the first term, we got the second part of the gradient of $X$:

$$\begin{aligned} \left(\frac{\partial L}{\partial X}\right)_{\sigma^2} = \left(\frac{2}{N} \mathbf{1}_N \frac{\partial L}{\partial \sigma^2}\right) \odot (X - \mathbf{1}_N\mu) \end{aligned}$$

For the second term, we got the second part of the gradient of $\mu$:

$$\begin{aligned} \left(\frac{\partial L}{\partial \mu}\right)_{\sigma^2} = -\left(\frac{2}{N} \mathbf{1}_N \frac{\partial L}{\partial \sigma^2}\right) \odot (X - \mathbf{1}_N\mu) \end{aligned}$$

Step 4: Backpropagate μ

Now we have $\frac{\partial L}{\partial \mu}$:

$$\begin{aligned} \frac{\partial L}{\partial \mu} = \left(\frac{\partial L}{\partial \mu}\right)_{\hat{X}} + \left(\frac{\partial L}{\partial \mu}\right)_{\sigma^2} \end{aligned}$$

Recall the formula of $\mu$:

$$\begin{aligned} \mu &= \frac{1}{N} \mathbf{1}_N^\top X \\ \end{aligned}$$

Hence,

$$\begin{aligned} d\mu &= \frac{1}{N} \mathbf{1}_N^\top dX \\ \end{aligned}$$

Therefore,

$$\begin{aligned} dL &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial \mu}\right)^\top d\mu\right) \\ &= \mathrm{tr}\left(\left(\frac{\partial L}{\partial \mu}\right)^\top \frac{1}{N} \mathbf{1}_N^\top dX\right) \\ \end{aligned}$$

Thus,

$$\begin{aligned} \left(\frac{\partial L}{\partial X}\right)_\mu = \frac{1}{N} \mathbf{1}_N \frac{\partial L}{\partial \mu} \end{aligned}$$

Final Step: Gradient of X

Finally, we have the gradient of $X$:

$$\begin{aligned} \frac{\partial L}{\partial X} = \left(\frac{\partial L}{\partial X}\right)_{\hat{X}} + \left(\frac{\partial L}{\partial X}\right)_{\mu} + \left(\frac{\partial L}{\partial X}\right)_{\sigma^2} \end{aligned}$$

Summary

Fig: Computational graph

Backpropagate $Y$:

$$\begin{aligned} \frac{\partial L}{\partial \gamma} &= \hat{X}^\top\mathbf{1}_N^\top\frac{\partial L}{\partial Y} \\ \frac{\partial L}{\partial \beta} &= \mathbf{1}_N^\top\frac{\partial L}{\partial Y} \\ \frac{\partial L}{\partial \hat{X}} &= \frac{\partial L}{\partial Y} \odot \mathbf{1}_N \gamma \\ \end{aligned}$$

Backpropagate $\hat{X}$:

$$\begin{aligned} \frac{\partial L}{\partial \sigma^2} &= -\mathbf{1}_N^\top\left(\frac{\partial L}{\partial \hat{X}} \odot \frac{(X-\mathbf{1}_N\mu)}{2(\mathbf{1}_N\sigma^2+\epsilon)^{\frac{3}{2}}}\right) \\ \left(\frac{\partial L}{\partial \mu}\right)_{\hat{X}} &= -\mathbf{1}_N^\top\left(\frac{\partial L}{\partial \hat{X}} \odot \frac{1}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}}\right) \\ \left(\frac{\partial L}{\partial X}\right)_{\hat{X}} &= \frac{\partial L}{\partial \hat{X}} \odot \frac{1}{\sqrt{\mathbf{1}_N\sigma^2+\epsilon}} \\ \end{aligned}$$

Backpropagate $\sigma^2$:

$$\begin{aligned} \left(\frac{\partial L}{\partial \mu}\right)_{\sigma^2} &= -\left(\frac{2}{N} \mathbf{1}_N \frac{\partial L}{\partial \sigma^2}\right) \odot (X - \mathbf{1}_N\mu) \\ \left(\frac{\partial L}{\partial X}\right)_{\sigma^2} &= \left(\frac{2}{N} \mathbf{1}_N \frac{\partial L}{\partial \sigma^2}\right) \odot (X - \mathbf{1}_N\mu) \\ \end{aligned}$$

Backpropagate $\mu$:

$$\begin{aligned} \frac{\partial L}{\partial \mu} &= \left(\frac{\partial L}{\partial \mu}\right)_{\hat{X}} + \left(\frac{\partial L}{\partial \mu}\right)_{\sigma^2} \\ \left(\frac{\partial L}{\partial X}\right)_{\mu} &= \frac{1}{N} \mathbf{1}_N \frac{\partial L}{\partial \mu} \end{aligned}$$

Finally, we have the gradient of $X$:

$$\begin{aligned} \frac{\partial L}{\partial X} = \left(\frac{\partial L}{\partial X}\right)_{\hat{X}} + \left(\frac{\partial L}{\partial X}\right)_{\mu} + \left(\frac{\partial L}{\partial X}\right)_{\sigma^2} \end{aligned}$$

Implementation

# Credits: This code is based on the assignment from UMich EECS 498-007/598-005 assignment 3

import torch
class BatchNorm(object):

    @ staticmethod
    def forward(x, gamma, beta, bn_param):
        """
        Forward pass for batch normalization.

        During training the sample mean and (uncorrected) sample variance
        are computed from minibatch statistics and used to normalize the
        incoming data. During training we also keep an exponentially decaying
        running mean of the mean and variance of each feature, and these
        averages are used to normalize data at test-time.

        At each timestep we update the running averages for mean and
        variance using an exponential decay based on the momentum parameter:

        running_mean = momentum * running_mean + (1 - momentum) * sample_mean
        running_var = momentum * running_var + (1 - momentum) * sample_var

        Note that the batch normalization paper suggests a different
        test-time behavior: they compute sample mean and variance for
        each feature using a large number of training images rather than
        using a running average. For this implementation we have chosen to use
        running averages instead since they do not require an additional
        estimation step; the PyTorch implementation of batch normalization
        also uses running averages.

        Input:
        - x: Data of shape (N, D)
        - gamma: Scale parameter of shape (D,)
        - beta: Shift parameter of shape (D,)
        - bn_param: Dictionary with the following keys:
          - mode: 'train' or 'test'; required
          - eps: Constant for numeric stability
          - momentum: Constant for running mean / variance.
          - running_mean: Array of shape (D,) giving running mean
            of features
          - running_var Array of shape (D,) giving running variance
            of features

        Returns a tuple of:
        - out: of shape (N, D)
        - cache: A tuple of values needed in the backward pass
        """
        mode = bn_param['mode']
        eps = bn_param.get('eps', 1e-5)
        momentum = bn_param.get('momentum', 0.9)

        N, D = x.shape

        # 如果字典中没有这两个 key，就返回 0
        # 但字典里并没有把对应的 key 添加进去
        running_mean = bn_param.get('running_mean',
                                    torch.zeros(D,
                                                dtype=x.dtype,
                                                device=x.device))
        running_var = bn_param.get('running_var',
                                   torch.zeros(D,
                                               dtype=x.dtype,
                                               device=x.device))

        out, cache = None, None
        if mode == 'train':
            ##################################################################
            # TODO: Implement the training-time forward pass for batch norm. #
            # Use minibatch statistics to compute the mean and variance, use #
            # these statistics to normalize the incoming data, and scale and #
            # shift the normalized data using gamma and beta.                #
            #                                                                #
            # You should store the output in the variable out.               #
            # Any intermediates that you need for the backward pass should   #
            # be stored in the cache variable.                               #
            #                                                                #
            # You should also use your computed sample mean and variance     #
            # together with the momentum variable to update the running mean #
            # and running variance, storing your result in the running_mean  #
            # and running_var variables.                                     #
            #                                                                #
            # Note that though you should be keeping track of the running    #
            # variance, you should normalize the data based on the standard  #
            # deviation (square root of variance) instead!                   #
            # Referencing the original paper                                 #
            # (https://arxiv.org/abs/1502.03167) might prove to be helpful.  #
            ##################################################################
            # Replace "pass" statement with your code
            # Compute the mean and variance of the mini-batch
            mean = x.mean(dim=0)
            var = x.var(dim=0, unbiased=False)
            std = torch.sqrt(var + eps)
            x_hat = (x - mean) / std
            out = gamma * x_hat + beta
            # Update cache
            cache = (x, mean, var, std, x_hat, gamma, beta, eps, mode)

            # Update running mean and variance

            # Wrong code
            # bn_param['running_mean'] = momentum * \
            #     mean + (1 - momentum) * running_mean
            # bn_param['running_var'] = momentum * \
            #     var + (1 - momentum) * running_var

            # Correct code
            # Why ? Because the professor has done the storage below !!!
            # And his implementation has rewritten what I have done...
            # I have been stuck here for a long time...
            # Read through the code before you start coding...

            running_mean = (1 - momentum) * mean + momentum * running_mean
            running_var = (1 - momentum) * var + momentum * running_var

            ################################################################
            #                           END OF YOUR CODE                   #
            ################################################################
        elif mode == 'test':
            ################################################################
            # TODO: Implement the test-time forward pass for               #
            # batch normalization. Use the running mean and variance to    #
            # normalize the incoming data, then scale and shift the        #
            # normalized data using gamma and beta. Store the result       #
            # in the out variable.                                         #
            ################################################################
            # Replace "pass" statement with your code
            std = torch.sqrt(running_var + eps)
            x_hat = (x - running_mean)
            out = gamma * x_hat + beta
            cache = (x, running_mean, running_var, std,
                     x_hat, gamma, beta, eps, mode)
            ################################################################
            #                      END OF YOUR CODE                        #
            ################################################################
        else:
            raise ValueError('Invalid forward batchnorm mode "%s"' % mode)

        # Store the updated running means back into bn_param
        bn_param['running_mean'] = running_mean.detach()
        bn_param['running_var'] = running_var.detach()

        return out, cache

    @ staticmethod
    def backward(dout, cache):
        """
        Backward pass for batch normalization.

        For this implementation, you should write out a
        computation graph for batch normalization on paper and
        propagate gradients backward through intermediate nodes.

        Inputs:
        - dout: Upstream derivatives, of shape (N, D)
        - cache: Variable of intermediates from batchnorm_forward.

        Returns a tuple of:
        - dx: Gradient with respect to inputs x, of shape (N, D)
        - dgamma: Gradient with respect to scale parameter gamma,
          of shape (D,)
        - dbeta: Gradient with respect to shift parameter beta,
          of shape (D,)
        """
        dx, dgamma, dbeta = None, None, None
        #####################################################################
        # TODO: Implement the backward pass for batch normalization.        #
        # Store the results in the dx, dgamma, and dbeta variables.         #
        # Referencing the original paper (https://arxiv.org/abs/1502.03167) #
        # might prove to be helpful.                                        #
        # Don't forget to implement train and test mode separately.         #
        #####################################################################
        # Replace "pass" statement with your code
        mode = cache[-1]
        if mode == 'train':
            x, mean, var, std, x_hat, gamma, beta, eps = cache[:-1]
            # var = x.var(dim=0, unbiased=False)
            # mean = x.mean(dim=0)
            # x_hat = (x - mean) / torch.sqrt(var + eps)
            # out = gamma * x_hat + beta
            N, D = x.shape
            dbeta = dout.sum(dim=0)
            dgamma = (dout * x_hat).sum(dim=0)
            dx_hat = dout * gamma
            dx = dx_hat / std
            dmu = -dx_hat.sum(dim=0) / std
            dsigma2 = torch.sum(-0.5 * dx_hat * x_hat / (std ** 2), dim=0)
            dmu += dsigma2 * torch.mean(-2 * (x - mean), dim=0)
            dx += dmu / N
            dx += dsigma2 * 2 * (x - mean) / N
        elif mode == 'test':
            x, running_mean, running_var, std, x_hat, gamma, beta, eps = cache
            dbeta = dout.sum(dim=0)
            dgamma = (dout * x_hat).sum(dim=0)
            dx_hat = dout * gamma
            dx = dx_hat / std
        #################################################################
        #                      END OF YOUR CODE                         #
        #################################################################

        return dx, dgamma, dbeta

    @ staticmethod
    def backward_alt(dout, cache):
        """
        Alternative backward pass for batch normalization.
        For this implementation you should work out the derivatives
        for the batch normalization backward pass on paper and simplify
        as much as possible. You should be able to derive a simple expression
        for the backward pass. See the jupyter notebook for more hints.

        Note: This implementation should expect to receive the same
        cache variable as batchnorm_backward, but might not use all of
        the values in the cache.

        Inputs / outputs: Same as batchnorm_backward
        """
        dx, dgamma, dbeta = None, None, None
        ###################################################################
        # TODO: Implement the backward pass for batch normalization.      #
        # Store the results in the dx, dgamma, and dbeta variables.       #
        #                                                                 #
        # After computing the gradient with respect to the centered       #
        # inputs, you should be able to compute gradients with respect to #
        # the inputs in a single statement; our implementation fits on a  #
        # single 80-character line.                                       #
        ###################################################################
        # Replace "pass" statement with your code
        x, mean, var, std, x_hat, gamma, beta, eps, mode = cache
        N, D = x.shape
        if mode == 'train':
            dbeta = dout.sum(dim=0)
            dgamma = (dout * x_hat).sum(dim=0)
            dx_hat = dout * gamma
            dx = (dx_hat - dx_hat.mean(dim=0) -
                  x_hat * (dx_hat * x_hat).mean(dim=0)) / std
        elif mode == 'test':
            dbeta = dout.sum(dim=0)
            dgamma = (dout * x_hat).sum(dim=0)
            dx = dout * gamma / std
        #################################################################
        #                        END OF YOUR CODE                       #
        #################################################################

        return dx, dgamma, dbeta